Sie sind hier:

Effektiver Jahreszinssatz nach PAngV (4): Die Ermittlung des Effektivzinssatzes

 zurück

Ausgangspunkt Ihrer Überlegungen bei Effektivzinsfragen sollte immer das
finanzmathematische Äquivalenzprinzip sein:
Die Leistung des Gläubigers entspricht der Leistung des Schuldners.

Leistung des Gläubigers = Leistung des Schuldners

(Vgl.   Anlage zu § 6 PAngV)

Leistungen und Gegenleistung müssen dabei auf einen gemeinsamen Zeitpunkt bezogen werden, damit sie tatsächlich vergleichbar werden.

Wählt man als gemeinsamen Bezugszeitpunkt den Zeitpunkt der Darlehensauszahlung, so sind die künftigen Ratenzahlungen des Darlehensnehmers und die Begleichung der am Ende der Zinsbindung noch offenen Restschuld auf den Zeitpunkt der Darlehensauszahlung abzuzinsen. Bei monatlicher Ratenzahlung ist die erste Rate also über einen Monat (=1/12 des Jahres), die zweite über zwei Monate usw. abzuzinsen.

In unserem Beispiel würde sich hieraus ergeben:

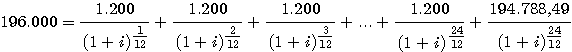
Die große Unbekannte ist natürlich die Zinsrate i, mit der abzuzinsen ist. Es ist die Zinsrate, die tatsächlich die Leistungen von Gläubiger und Schuldner gleichwertig werden läßt, der als Dezimalzahl ausgedrückte Effektivzinssatz.
Bevor Sie sich in dem fruchtlosen Versuch aufopfern, die obige Gleichung nach i aufzulösen - probieren Sie einfach! Setzen Sie Versuchszinssätze ein und nähern Sie sich damit dem gewünschten Ergebnis an. Ich bin dabei auf einen Zinssatz von rund 7,291153517% gekommen - alles klar?

Auch Kalkulationsprogramme gehen im Prinzip nicht anders vor, nur eben schneller :-).
Zwei Möglichkeiten, wie Sie hier MS-Excel einschalten können, habe ich Ihnen in einer -Datei beschrieben.

Falls Sie angehalten sind, das Problem manuell mit Hilfe eines Taschenrechners zu lösen, können Sie zweckmäßigerweise so vorgehen:

Zinsen Sie die Schuldnerzahlungen statt mit dem Jahreszinssatz mit dem konformen Monatszinssatz ab:

 

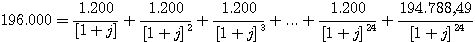
Jetzt können Sie auf Ihre Kenntnisse aus der Rentenrechnung zurückgreifen und den Rentenbarwertfaktor anwenden, so daß Sie eine ganz wesentliche Vereinfachung des Formelmonstrums erreichen: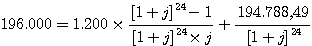
 

Formen Sie um: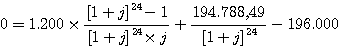
 
Sie müssen also den konformen Monatszinssatz suchen, der die Differenz zwischen den barwertigen Leistungen des Darlehensnehmers und den barwertigen Leistungen des Darlehensgebers gleich 0 werden läßt (suchen Sie also den internen Zinsfuß als Monatszinssatz).
Ich bezeichne diese Differenz im weiteren mit dem Symbol C. Wer sich in der Investionsrechnung auskennt, wird hierin unschwer den Kapitalwert erkennen.

Gehen Sie nun nach dem Versuch-Irrtum-Prinzip vor. Versuchen Sie mit einem Zinssatz Ihrer Wahl dahin zu gelangen, daß C tatsächlich den Wert 0 annimmmt.
Setzen Sie z.B. zunächst einen Zinssatz von 0,5% an so ergibt sich ein C von 3.889 (aus j₁ = 0,005 resultiert also ein C₁ von +3.889).
Starten Sie einen zweiten Versuch mit einem j₂ = 0,006, so errechnen Sie hieraus ein C₂ von -514,89.
Sie haben nun zwei Wertepaare erhalten, zwischen denen Sie linear interpolieren können.
Die rechnerische lineare Interpolation kann vorgenommen werden mit Hilfe der Formel
 
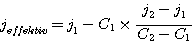
Setzen Sie die ermittelten Versuchswerte ein, und Sie erhalten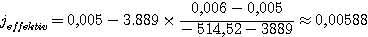

Abschließend muß noch der so ermittelte konforme Monatszinssatz j in den entsprechenden Jahreszinssatz i umgerechnet werden.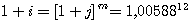

 

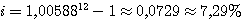
PangV (1): Inhalt und Lösungsschritte

PangV (2): Der Tilgungsplan der Bank

PAngV (3): Das Vergleichskonto nach PAngV

PAngV (4): Die Ermittlung des Effektivzinssatzes

PAngV (5): Eine mögliche Interpretation des Annuitätendarlehens

 zurück