Sie sind hier:

Effektiver Jahreszinssatz nach PAngV (3): Das Vergleichskonto nach PAngV

 zurück

Die Modalitäten, nach denen Zins- und Tilgungsverrechnungen in den Tilgungsplan der Bank einfließen, sind Vertragsgegenstand. Sie können also durchaus in jedem Falle spezifisch ausgestaltet werden. Kreditverträge sind folglich nur sehr bedingt miteinander vergleichbar. Auch bei scheinbar gleichen Konditionen können unterschiedliche Belastungen für den Kreditnehmer entstehen.

vgl. unterschiedliche Varianten der Zins- und Tilgungsverrechnung

Demgegenüber wird durch den Gesetzgeber in der Preisangabeverordnung zwingend ein einheitliches Abrechnungsmodell vorgegeben, um den Vergleich zu ermöglichen.

(vgl. § 6 PAngV)

Beim Aufstellen des Vergleichskontos nach Preisangabenverordnung gilt:

1. Es sind die tatsächlichen Zahlungen des Kreditgebers und des Kreditnehmers zugrundezulegen.
Die Vergleichsrechnung beginnt deshalb mit dem effektiv ausgezahlten Darlehensbetrag (im Beispiel nur 98% des vertraglich fixierten Darlehensbetrages, also 196.000 EUR). 

2. Alle Leistungen sind taggenau abzurechnen.
Unabhängig von den vertraglichen Vereinbarungen werden im Vergleichskonto die Zahlungen zu dem Zeitpunkt zins- und tilgungswirksam verrechnet, in dem sie geleistet werden.
Die gezahlte Rate vermindert die Restschuld des Darlehensnehmers sofort.
Im gleichen Zeitpunkt wird dem Darlehensnehmer der Preis für die Kreditinanspruchnahme während zurückliegenden Periode - also der Zins - in Rechnung gestellt. Für die Zeitberechnung gilt: Das Jahr wird mit 365 bzw. 366 Tagen oder 52 Wochen oder 12 gleich langen Standardmonaten angesetzt. Ein Standardmonat hat eine Länge von ³⁶⁵/₁₂ Tagen = 30,41666 Tagen (unabhängig davon, ob es sich um ein Schaltjahr handelt). Dieser Zins wird dem künftig zu verzinsenden Kapital zugeschlagen (kapitalisiert). Bei unterjähriger Ratenzahlungen resultiert aus dieser Vorgehensweise ein unterjähriger Zinseszinseffekt, der nach neuer Preisangabenverordnung im effektiven Jahreszins berücksichtigt wird. Die PAngV legt deshalb fest:

3. Auch im unterjährigen Bereich ist exponentiell zu rechnen.
Der angegebene Effektivzinssatz ist ein Jahreszinssatz. Wenn monatliche oder quartalsweise Ratenzahlungen erfolgen, müssen die Zinsen für den zurückliegenden Monat bzw. das zurückliegende Quartal berechnet werden. Hierzu wird der entsprechende Monats- bzw. Quartalszinssatz benötigt. Der Jahreszinssatz muß in einen unterjährigen Periodenzinssatz umgerechnet werden. Dieser muß zum gleichen Ergebnis führen wie der Jahreszinssatz.
Also: wenn ein Anfangskapital K0 genau 1 Jahr lang verzinst wird, so muß das Endkapital Km gleichhoch sein - gleichgültig ob einmal mit der Jahreszinsrate i (= Zinssatz/100) oder m-mal mit der konformen Periodenzinsrate jkonform aufgezinst wurde: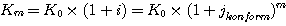

Durch Umstellen erhält man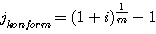

nähere Erläuterungen zum Problem unterjähriger Zinsrechnung

Im vorliegenden Beispiel sind gegeben

a) der effektive Jahreszinssatz mit 7,29%, als Rate ausgedrückt 0,0729

b) 12 Zinsberechnungen innerhalb eines Jahres.

Hieraus kann zunächst der zum Jahreszinssatz konforme Monatszinssatz bestimmt werden
 

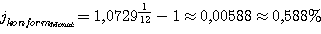
Probe:
100 EUR, einmal verzinst mit 7,29 % p.a., wachsen in einem Jahr auf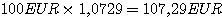

100 EUR, monatlich mit 0,588 % und Zinseszins verzinst, wachsen auf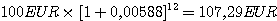

Beachten Sie bitte den Unterschied zum relativen Monatszinssatz, der in der üblichen kaufmännischen Rechnung, so auch im Tilgungsplan der Bank, Anwendung findet. Dort wäre zu rechnen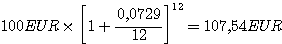

 Auf Basis der geschilderten Vorgehensweise kann nun das Vergleichskonto nach PAngV aufgestellt werden.

Anmerkung:
Das nachfolgende Vergleichskonto wurde nicht mit gerundeten, sondern exakten Werten des effektiven Jahreszinssatzes bzw. des konformen Monatszinssatzes durchgerechnet. Falls Sie jetzt also manuell nachrechnen, werden Sie u.U. geringfügig abweichende Ergebnissse erhalten.

Bis auf eine vernachlässigbare Rundungsdifferenz stimmt die Restschuld am Ende der Zinsbindung beim Vergleichskonto nach PAngV mit der des Tilgungsplans der Bank überein. Der anfängliche effektive Jahreszinssatz wurde somit korrekt angegeben.

PangV (1): Inhalt und Lösungsschritte

PangV (2): Der Tilgungsplan der Bank

PAngV (3): Das Vergleichskonto nach PAngV

In Kenntnis der Funktionsweise des PAngV-Modells ist es relativ einfach, den effektiven Jahreszins auf eigene Faust zu ermitteln ...

PAngV (4): Die Ermittlung des Effektivzinssatzes

PAngV (5): Eine mögliche Interpretation des Annuitätendarlehens

  zurück