Beispiel:
Sie legen 100 € an. Für die Verzinsung wird ein nomineller Jahreszinssatz von 6 % p.a. angegeben.

Fall 1: Der Zinszuschlag erfolgt genau 1 Jahr nach erfolgter Anlage.
Ihr Kapital wächst dadurch auf 100 € + 100 € x 6/100 = 100 € x 1,06 = 106 €.
Die tatsächlich (effektiv) erreichte Verzinsung entspricht der nominellen (6 %).

Fall 2: Der Zinszuschlag erfolgt monatlich (z.B. auf einem Festgeldkonto). Die Zinsen werden also zu jedem Monatsende dem Kapital zugeschlagen und im Folgemonat mitverzinst.
Die Zinsen für den ersten Monat werden berechnet. Sie erhalten üblicherweise 1/12 der Jahreszinsen, also  (100 € x 6/100)/12 = 100 € x 0,5/100 = 0,5 €.
Das Kapital ist also innerhalb eines Monats von 100 € auf 100,5 € angewachsen, wurde also mit
6%/12 = 0,5 % pro Monat verzinst.

Dieser Zinssatz ist ein relativer Periodenzinssatz (im Beispielfall ein relativer Monatszinssatz).
Er wird errechnet nach Nomineller Jahreszinsatz/Anzahl der Verzinsungen pro Jahr.

Das nach dem ersten Zinszuschlag vorhandene Kapital kann also auch direkt unter Nutzung des relativen Monatszinssatzes errechnet werden:
100 € + 100 € x 0,5/100 = 100 € x 1,005 = 100,5 € (also das 1,005-fache des Anfangskapitals).
 

Wie vollzieht sich das weitere Kapitalwachstum?
Im zweiten Monate werden 100,5 € mit 0,5 % verzinst. Der Endwert nach zwei Monaten beträgt dann 100,50 € x 1,005 = 101,0025 €.
Man kann natürlich auf direktem Wege vom Ursprungskapital auf des am Ende des zweiten Monats vorhandene Kapital schließen. Das Anfangskapital wurde zwei mal mit dem Faktor 1,005 multipliziert: 100 x 1,005 x 1,005 = 100 x 1,005² = 100,0025.

Wollen Sie bestimmen, auf welchen Betrag Ihr Kapital innerhalb eines Jahres (also durch 12 Verzinsungen) anwächst, können Sie das analog berechnen:
100 x 1,005¹² = 106,1678

Verallgemeinerung:

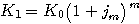
mit

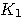
Endkapital nach einem Jahr

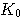
Anfangskapital

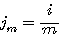
relative Periodenzinsrate,

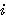
nominelle Jahreszinsrate
= nomineller Jahreszinssatz/100

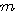
Anzahl der Verzinsungen pro Jahr

Wenn Sie wissen wollen, welches Endkapital sich ergibt, wenn der beschriebene Prozeß gleichbleicbend über mehrere Jahre abläuft, modfizieren Sie die Formel:

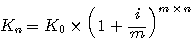
wobei n für die Anzahl der Jahre steht.

Zurück zu dem Zahlenbeispiel:
Das Anfangskapital von 100 € ist innerhalb eines Jahres auf 106,17 € angewachsen. Es hat sich also mit 6,17 % p.a. verzinst - der tatsächliche (effektive) Jahreszinssatz weicht somit vom angegebenen nominellen Jahreszinssatz ab.

Nicht in jedem Falle ist es möglich, den effektiven Jahreszins so einfach abzulesen.

 Deshalb die folgenden Hinweise zu dieser Problematik.