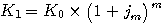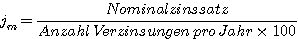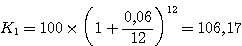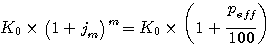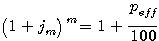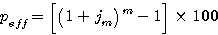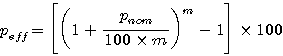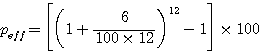|
|
x (1+ieff) |
|
||||||||
|
|
K1 |
|||||||||
| K0 x (1+jm)
|
x (1+jm)
|
x (1+jm)
|
... |
x (1+jm)
|
|
|||||
|
|
1
Zinsperiode |
|
... |
|
|
|||||
|
|
1 Jahr = m Zinsperioden |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|