Sie sind hier:

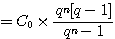
Annuitätenmethode

zurück

Die Annuitätenmethode dient dazu, einen finanzmathematischen durchschnittlichen jährlichen Überschuß zu ermitteln.

Während die Kapitalwertmethode einen Totalerfolg bestimmt (wieviel Gewinn wird zusätzlich zur kalkulierten Verzinsung erreicht), wird bei der Annutitätenmethode dieser Erfolg periodisiert. Hierzu wird der barwertige Gewinn (also der Kapitalwert) rechnerisch mit Hilfe des Annuitätenfaktors gleichmäßig über den Investitionszeitraum verteilt:

Annuität oder
finanzmathematischer durchschnittlicher jährlicher Überschuß DJÜ

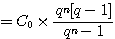
Für das Beispielangebot B beträgt die

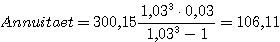
Zur Veranschaulichung eignet sich folgender Tilgungsplan, in welchem das Investitionsobjekt seine Schulden beim Investor abträgt, das jeweils gebunden Kapital mit dem Kalulationszinssatz verzinst und darüber hinaus einen gleichbleibenden Überschuss erwirtschaftet.

Wir könnten also jährlich gleichbleibend 106,11 € aus dem Investitionsprozess entnehmen. Die Ertragskraft des Investitionsobjekts reicht aus, um trotz dieser Entnahme die kalkulierte Verzinsung zu erwirtschaften und den investierten Betrag vollständig zurückzuerstatten.

Oder:
Wenn sich die künftigen Überschüsse gegenüber unseren Erwartungen in jeder Periode um 106,11 € verringern würden, würde die kalkulierte Verzinsung gerade noch erreicht.

Die Lösung für das Beipielangebot A finden Sie HIER.

Am Beispiel ist erkennbar, was ein positiver DJÜ bedeutet:

• der Investor gewinnt sein eingesetztes Kapital zurück,
• er erhält eine Verzinsung in Höhe des Kalkulationszinssatzes, und
• er erhält darüber hinaus im Jahresdurchschnitt einen
  konstanten Überschuß (extra profit) in Höhe des DJÜ.

Umgekehrt erleidet der Investor bei einem  negativen DJÜ - gemessen an der kalkulierten Verzinsung - einen Durchschnittsverlust je Rechnungsperiode in eben dieser Höhe.

 zurück