Sie sind hier:

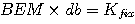
Ermittlung der Break-Even-Menge

 zurück

Bei welcher Menge wird die Gewinnschwelle erreicht, wenn die Preise gegeben sind?

Beispiel:

Jedes verkaufte Stück erbringt somit einen Beitrag zur Deckung der fixen Kosten in Höhe von

4,20 €/Stück - 2,00 €/Stück = 2,20 €/Stück = db.

Zur vollständigen Kostendeckung wird ein Deckungsbeitrag in Höhe der fixen Kosten (50.000 €) benötigt. Zur Erwirtschaftung dieses Betrages muß eine bestimmte Menge des Erzeugnisses (die Break-Even-Menge BEM) abgesetzt werden, wobei jedes Erzeugnis den berechneten Deckungsbeitrag je Stück (db) erbringt:

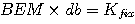
Daraus folgt

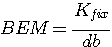
Im Beispiel ist also zu rechnen

Es müssen also mehr als 22.727 Stück pro Jahr produziert und abgesetzt werden, um in die Gewinnzone zu gelangen.

Sicherheitsspanne - mengenbezogen -

Auf Basis der ermittelten Break-Even-Menge lassen sich nun weitere Überlegungen unter Sicherheitsapekten anstellen.

Wenn das Unternehmen im Ergebnis einer Marktanalyse plant, künftig 30.000 Stück/Jahr abzusetzen, dann beträgt die

Sicherheitsspanne_absolut  = Geplante Mege - BEM

= 30.000 Stk/Jahr - 22.728 Stück/Jahr = 7.272 Stück/Jahr

Sicherheitsspanne_relativ (ausgedrückt in Prozent der geplanten Menge)
 

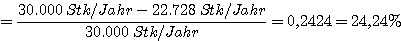
Im Planungsprozeß kann natürlich auch eine Sicherheitsspanne zur Ermittlung der zu planenden Mindestabsatzmenge vorgegeben werden.

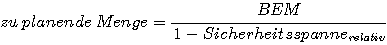
im Beipiel:

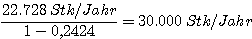
Es ist dann zu prüfen, ob diese Menge im gegebenen Markt und mit den vorhandenen Kapazitäten erreicht werden kann.

BEM-Rechner